The Election Commission of India (ECI) has attracted criticism for reducing the Voter Verified Paper Audit Trail (VVPAT) based audit of Electronic Voting Machines (EVMs) to an exercise in tokenism and for its lack of transparency in the matter. The uniform sample size of “five EVMs per Assembly constituency” prescribed by it for all Assembly constituencies and States does not conform to the fundamental principles of statistical sampling and leads to high margins of error.
At the same time, the ECI’s critics are also guilty of demanding arbitrary, non-statistical sample sizes like “25 per cent samples” and “50 per cent samples” for VVPAT-based audit of EVMs, under the mistaken impression that a “bigger percentage” guarantees greater accuracy of results. Some are now demanding a 100% manual count of all VVPAT voter slips.
Using statistical sampling
The VVPAT-based audit of EVMs is a simple problem of statistical quality control. It is very similar to the “lot acceptance sampling technique” that is widely used in industry and trade. If the number of defectives found in a randomly drawn statistical sample is less than or equal to a specified acceptance number, the lot (or ‘population’) is accepted; otherwise, the lot is rejected.
Here a ‘defective EVM’ is defined as one with a mismatch between the EVM count and the VVPAT’s manual count of voter slips due to EVM malfunction or EVM manipulation. Unlike industry and trade where a few defectives in the sample may be tolerated, in the context of elections, the acceptance number will have to be ‘zero defective EVM’. In other words, even if there is a single instance of mismatch between the EVM count and VVPAT manual count in the randomly drawn sample of EVMs, the ‘population’ of EVMs from which the sample was drawn should be ‘rejected’. In this case, ‘rejection’ means non-acceptance of the EVM counts for that ‘population’ and doing manual counting of VVPAT slips for all the remaining EVMs of that ‘population’. In such a scenario, the election result should be declared only on the basis of the VVPAT count.
Thus, VVPAT-based audit of EVMs involves three essential elements — (a) a clear definition of the ‘population’ of EVMs from which the statistical sample would be drawn. It could be all the EVMs deployed in an Assembly constituency, a Parliamentary constituency, a State as a whole, India as a whole, a region (or group of districts) within a State, or any other. The population size (N) could vary widely depending on how we define the ‘population’; (b) determination of a statistically correct and administratively viable sample size (n) of EVMs whose VVPAT slips will be hand counted; (c) application of the ‘decision rule’, viz., in the event of a mismatch between the EVM count and the VVPAT count in the chosen sample of ‘n’ EVMs, the hand counting of VVPAT slips will have to be done for all the remaining (N-n) EVMs forming part of that ‘population’.
However, the ECI has not specified the ‘population’ to which its sample size relates. It has not explained how it arrived at its sample size. It has maintained silence about the ‘next steps’ in the event of a mismatch between the EVM count and the VVPAT count in the chosen sample, and it has glossed over reported cases of mismatch. A system of VVPAT-based audit of EVMs in which these three vital issues have been left vague or unaddressed is categorically unacceptable.
Why ECI’s sample size is erroneous
The hypergeometric distribution model should form the basis of the sampling plan for the VVPAT-based audit of EVMs because it is an exact fit. In the discussion that follows, we assume the percentage of defective EVMs in the population (P) to be 1%, and calculate sample sizes, for various population sizes, for 99% probability of detecting at least one defective EVM. We also compute the probability that the ECI-prescribed sample size of “five EVMs per Assembly constituency” will fail to detect a defective EVM for different population sizes. The great merit of the hypergeometric distribution model is that the sample size is the greatest when P is very close to zero (which is what the ECI claims it is), and it becomes lesser as P increases.

As seen from Table 1, when the population size (N) of EVMs is 100, the sample size (n) required is 99, that is it is nearly as big as the population size. As N increases, n also increases but at a much slower rate and ‘hits a plateau’ beyond some point so that further increases in population size have no effect on the sample size.
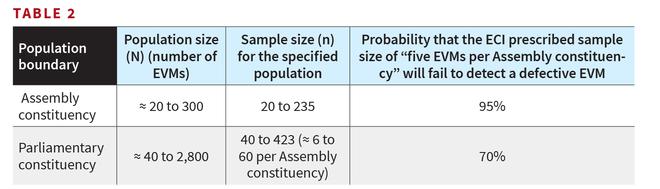
As seen from Table 2, if we define the EVMs deployed in an Assembly constituency or Parliamentary constituency as the ‘population’, then in view of the smaller population sizes (N), the sample sizes (n) required are rather big. Hence, both these choices for ‘population’ are administratively unviable.
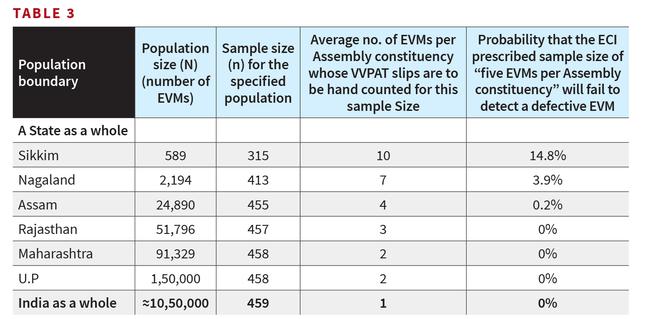
As seen from Table 3, if we define the EVMs deployed in a State as a whole or India as a whole as the ‘population’, then in view of the bigger population sizes (N), the sample sizes (n) required are very small. But the workload involved in hand counting the VVPAT slips for all the remaining (N-n) EVMs of the population, in the event of a mismatch, is very large and administratively unviable for India as a whole and for all States except the smaller States. The ECI glosses over this crucial point when it claims that the ISI, Kolkata had recommended a sample size of only 479 EVMs for India as a whole which works out to one EVM per Assembly constituency.
What next?
We can use the ‘plateau effect’ of sample sizes to divide the bigger States into ‘regions’ (an integral number of districts) with EVM population sizes of about 5,000 each. We treat “EVMs deployed in the region” as the ‘population’. On average, there would be about 20 Assembly constituencies in a region. The sample size required is 438 and the average number of EVMs per Assembly constituency whose VVPAT slips are to be hand counted is 22. For example, U.P with 1,50,000 EVMs can be divided into 30 regions with roughly 5,000 EVMs each. In the event of a defective EVM turning up, the hand counting of VVPAT slips of the remaining EVMs will confined to the region. This option is statistically robust and administratively viable.
Over the years, the Supreme Court has been indulgent towards the ECI due to its plenipotentiary role in the conduct of elections under Article 324 of the Constitution of India. But the Supreme Court cannot continue to turn a blind eye to the ECI making a mockery of the VVPAT-based audit of EVMs thereby defeating the very purpose of introducing the VVPAT. It must compel the ECI to make public how it has defined the population, how it has arrived at its sample size, and most importantly, its decision rule in the event of a mismatch. Only then, the Supreme Court’s order of 2013 on VVPAT would be implemented faithfully in letter and spirit.
The writer is a former IAS officer and former Vice Chancellor of the Indian Maritime University, Chennai







